Summary: Today’s activity…
Homework: none
Summary: Today’s activity…
Homework: Complete the Slides Above
Summary: Today we learned about infinite series.
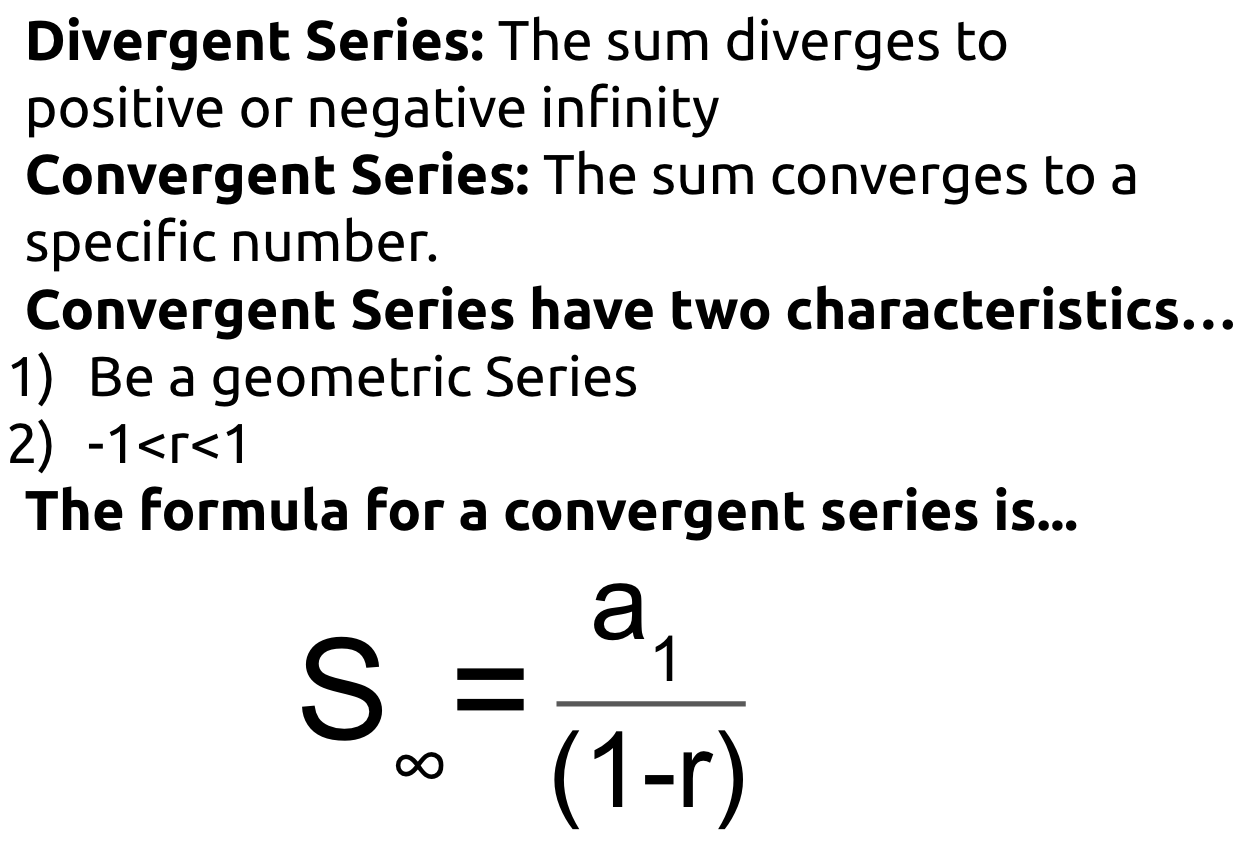
Homework: none (Test on Friday)
Summary: Today is a day to work on past work that you may have not yet completed. Today’s Agenda…
Homework: See above
Summary: Today we learned some shortcuts to find the sum of long series. See some in class examples here. Or see more examples here. Today we only covered arithmetic series.
Homework: HW04 (Due Monday)
Summary: Today we had a substitute teacher and practiced some series problems. See below (CA07)…
Also consider going back and completing two other activities from last week.
Summary: Today we learned some shortcuts to find the sum of long series. See some in class examples here. Or see more examples here. Today we only covered arithmetic series.
Homework: HW
Summary: Today we learned how to analyze sequences even if the given terms are nonconsecutive. See a PDF of examples here (1, 2). Or watch the video examples below…
Today’s activity (CA06)…
Homework: Complete the Slides in Today’s Activity (due by the end of class on Wednesday 1/29) *
Summary: Today’s activity (CA05)…
Also you may want to take this time to enter your Test Corrections.
Homework: Today’s Slide (due by the end of class on Wednesday 1/29)